12th Maths Guide Chapter 2 Complex Numbers Exercise 2.6 PDF Solution

Question no 1:

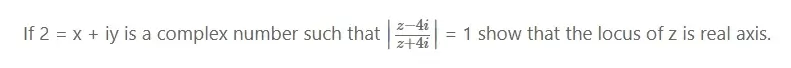
Solution:

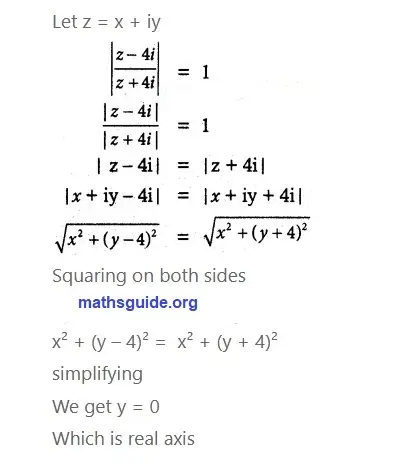
Question No 2:

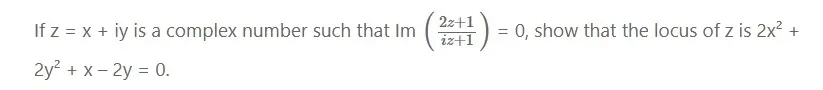
Solution:

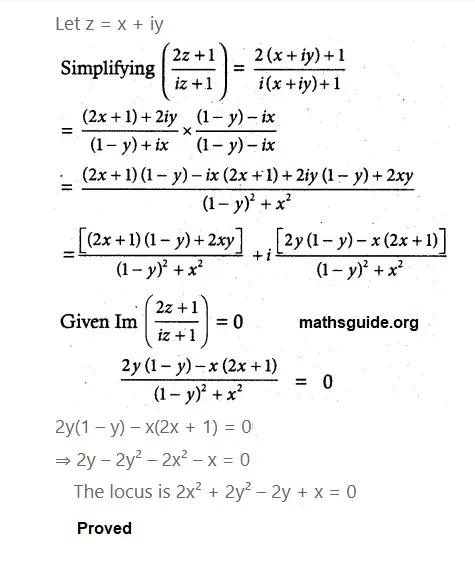
Question No 3: Obtain the Cartesian form of the locus of z = x + iy in each of the following cases.

(i) [Re (iz)]² = 3

Solution:

z = x + iy
[Re(iz)]² = 3
[Re[i(x + iy]]² = 3
[Re(ix – y)]² = 3
(-y)² = 3
y² = 3

(ii) Im[(1 – i)z + 1] = 0

Solution:

Im [(1 – i)(z + iy) + 1] = 0
Im[x + iy – ix + y + 1] = 0
Im[(x + y + 1) + i(y – x)] = 0
Considering only the imaginary part
y – x = 0 ⇒ x = y

(iii) |z + i| = |z – 1|

Solution:

|x + iy + i| = | x + iy – 1|
|x + i(y + 1)| = |(x – 1) + iy|
Squaring on both sides
|x + i(y + 1)|² = |(x – 1) + iy|²
x² + (y + 1)² = (x – 1)² + y²
x² + y² + 2y + 1 = x² – 2x + 1 + y²
2y + 2x = 0
x + y = 0

(iv) z¯ = z^-1

Solution:

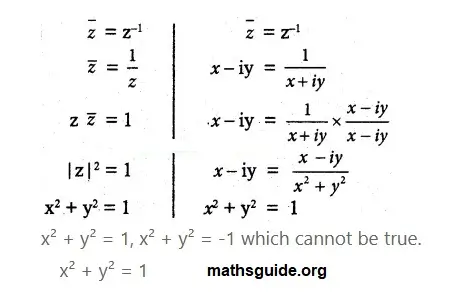
Question No 4: Show that the following equations represent a circle, and find its centre and radius.

(i) |z – 2 – i| = 3

Solution:

(ii) |2(x + iy) + 2 – 4i| = 2

Solution:

(iii) |3(x + iy) – 6 + 12i| = 8

Solution:

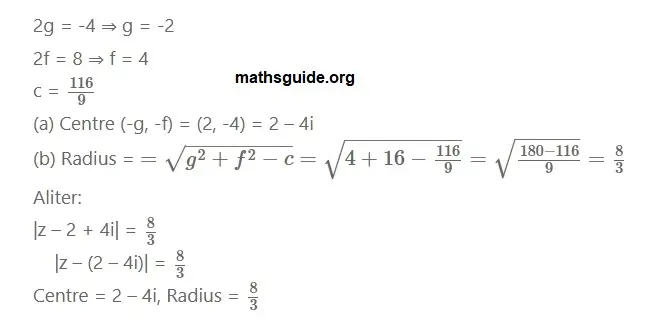
Question No 5: Obtain the Cartesian equation for the locus of z = x + iy in each of the following cases.

(i) |z – 4| = 16

Solution:

(ii) |z – 4|² – |z – 1|² = 16

Solution:

|x + iy – 4|² – |x + iy – 1|² = 16
|(x – 4) + iy|² – |(x – 1) + iy|² = 16
[(x – 4)² + y²] – [(x – 1)² + y²] = 16
(x² – 8x + 16 + y²) – (x² – 2x + 1 + y²) = 16
x² + y² – 8x + 16 – x² + 2x – 1 – y² = 16
-6x + 15 = 16
6x + 1 = 0
The locus of the point is a straight line.