12th Maths Guide Solution Application of Matrices and Determinants Exercise 1.6

Question no 1:

Test for consistency and if possible, solve the following systems of equations by rank method.
(i) x – y + 2z = 2, 2x + y + 4z = 7, 4x – y + z = 4

Solution:-

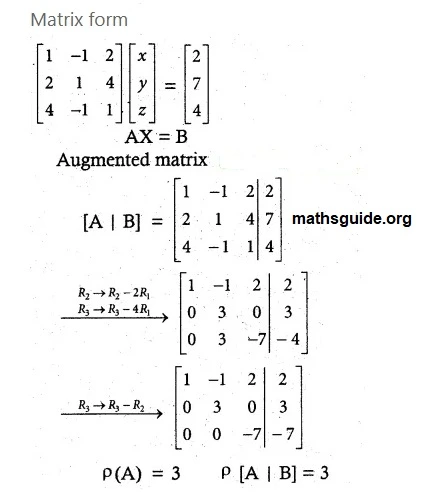
(ii) 3x + y + z = 2, x – 3y + 2z = 1, 7x – y + 4z = 5

Solution:-

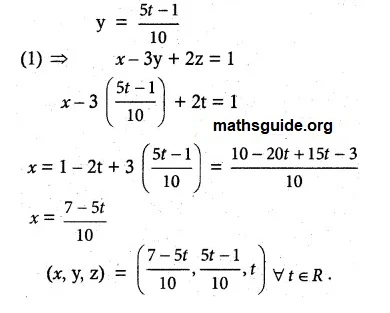
(iii) 2x + 2y + z = 5, x – y + z = 1, 3x + y + 2z = 4

Solution:-

(iv) 2x – y + z = 2, 6x – 3y + 3z = 6, 4x – 2y + 2z = 4

Solution:-

Question no 2: Find the value of k for which the equations is kx – 2y + z = 1, x – 2ky + z = -2, x – 2y + kz = 1 have

(i) no solution
(ii) unique solution
(iii) infinitely many solution.

Solution:-

Question no 3: Investigate the values of λ and µ the system of linear equations 2x + 3y + 5z = 9, 7x + 3y – 5z = 8, 2x + 3y + λz = µ, have

(i) no solution
(ii) a unique solution
(iii) an infinite number of solutions.

Solution:-